Hoe groot moet mijn experiment zijn?

03/03/2017

---

Regelmatig komt vanuit onze klanten in de Research & Development hoek de volgende vraag: “We gaan een nieuw experiment doen, wat zegt de statistiek over hoe groot mijn ‘N’ moet zijn? ‘N’ is hier de grootte van het experiment: hoeveel vrijwilligers heb je nodig in een test over hoe effectief een consumentenproduct is, of hoeveel runs in een fabriek zijn nodig om de volgende stap in het ontwerp van een nieuw productieproces te testen? En inderdaad, de statistiek heeft zoiets als 'sample size calculations', die achter knopjes in de gebruikte statistieksoftware zitten.

 

Stapje terug: wat is de situatie?

Op allerlei gebieden wordt geëxperimenteerd. Het doel is om een uitspraak te doen over de werkelijkheid, om iets te leren. Hierbij maken we onderscheid tussen de populatie en steekproef, twee bekende woorden uit het statistisch jargon. In het geval van onderzoek met mensen denken we bij de populatie aan de groep van alle mensen, nu en/of in de toekomst, die binnen het studie-onderwerp passen. Bijvoorbeeld: bezoekers aan een bepaalde supermarkt, patiënten met een bepaald kenmerk of alle kiesgerechtigden in een land. Bij onderzoek in een fabriek is de populatie bijvoorbeeld alle producten die een productieproces de komende jaren zal uitspugen. We kunnen niet de hele populatie bestuderen en daarom nemen we een steekproef uit de populatie, en die gaan we dan onderzoeken. We verzamelen data, doen een statistische analyse en doen vervolgens een uitspraak over de hele populatie. De steekproef zelf vinden we op zichzelf niet interessant, want we gaan niet een heel nieuw product ontwikkelen voor alleen de 50 mensen die aan de test hebben meegedaan.

 

Motivatie van de steekproefgrootte

We gaan er vanuit dat er in de planningsfase van het experiment een testplan ligt en er een doel is geformuleerd. Voor een training heb ik bijvoorbeeld het volgende overzicht gemaakt.

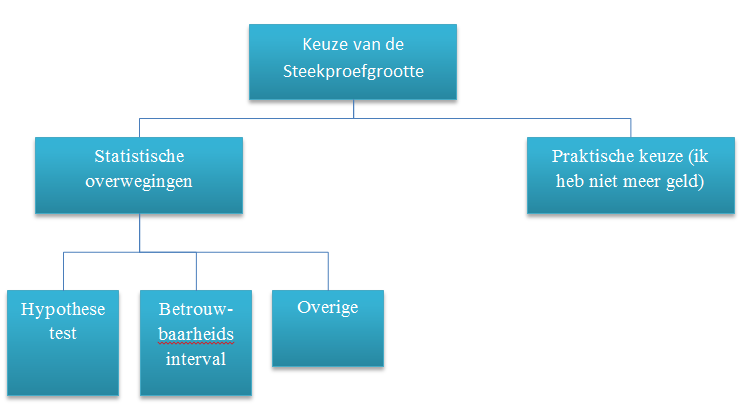
Het kan zijn dat de omstandigheden gewoon dicteren dat je test maar beperkt kan zijn. Een collega gaf wel eens als reactie: “hoeveel personen laten je projectbudget toe – dan wordt dat je steekproefgrootte”.

Maar met statistiek kun je een beter beeld krijgen van hoe je je steekproefgrootte moet bepalen om zinvolle resultaten te kunnen bereiken. Hiervoor zal je iets moeten aannemen over hoe de werkelijkheid in elkaar zit, en vooral: je moet een analyseplan hebben. Het schema geeft drie richtingen.

1. Hypothese testen. De meeste bekende theorieën en cursussen gaan over de hypothese-testen (met de beroemde p-waarden). Dit levert dan een ja-nee antwoord op: is er bewijs voor een verschil of effect? Is het verschil tussen oud en nieuw proces ‘significant’? (statistisch jargon). Ook kun je denken aan marketing claims: met ons product wordt je was bewijsbaar schoner.
2. Betrouwbaarheidsintervallen (in het Engels ‘confidence intervals’). Veel statistici vinden dat deze meer gebruikt zouden moeten worden. Ze leveren conclusies op van de vorm “we schatten het effect of verschil op 3.2, met een onzekerheid van 3.2 plus of min 1.2 (een 95% betrouwbaarheidsinterval).” Het effect kan dus overal tussen 2.0 en 4.4 liggen, met 95% ‘betrouwbaarheid’. Een ander voorbeeld: stel de analyse levert een betrouwbaarheidsinterval voor het effect van een interventie op van 0.8 +-1.2. Dan kan het effect dus zowel positief of negatief zijn. Maar het interval beperkt wel hoe negatief of hoe positief het effect is.
3. Overige: Denk hierbij aan een test waarbij het doel is om een complex model of algoritme te ontwikkelen, waar je wel voorbeelddata voor nodig hebt. Bijvoorbeeld om röntgenfoto’s automatisch te verwerken. Als je begint met het spelen met imaging technieken, heb je wel voorbeeldplaatjes nodig.

 

Rekenen en aannames

Voor de hypothese-testen en betrouwbaarheidsintervallen zijn er verschillende tools die voor allerlei situaties een steekproef kunnen uitrekenen. Een lastig punt hierbij is dat je wel iets moet aannemen over hoe de werkelijkheid in elkaar zit, bijvoorbeeld door bestaande expertise, een kleine pilot test, of eerder soortgelijk onderzoek. Je moet iets aannemen over het werkelijke verschil of effect, en meestal ook iets over de spreiding. Vanaf hier wordt het al snel meer technisch.

Bij betrouwbaarheidsintervallen hoef je doorgaans minder aannames te doen, vaak nog wel de spreiding¹.

 

Tenslotte: inzichten in het probleem

Het bovenstaande schetst de rekenkant van het verhaal. Regelmatig heb ik afspraken naar aanleiding van de vraag “hoe groot moet de test zijn”. Eigenlijk is de rekensom en de input daarvoor maar een klein onderdeel van het gesprek; meestal gaat het over wat er nu aan de hand is, en hoe dit vertaald kan worden naar een hypothese. Vaak is dat nog niet zo duidelijk en gebeuren daar juist de echt diepe dingen. Het levert ook een scherper beeld van hoe de analyse er uit kan zien. Als die aspecten zijn opgehelderd, is de berekening vaak nog maar een formaliteit die snel is opgelost.