23/01/2018

---

Kaggle Santa Challenge: Onze weg naar een gouden medaille!

Voor de vierde keer op rij streed CQM mee in de jaarlijkse optimalisatie uitdaging van Kaggle. Traditioneel betreft het een fictief maar moeilijk optimalisatie probleem van de Kerstman. Het probleem is fictief maar zeker geen kinderspel. Lees in deze blog hoe we met onze praktische ervaring in het toepassen van wiskunde de 7^de plek hebben behaald en daarmee een gouden medaille wonnen.

De oorspronkelijke uitdaging van Kaggle: Santa Gift Matching

Kaggle daagt ons uit om een algoritme te ontwikkelen voor het koppelen van cadeautjes aan kinderen zodat het geluk van de kinderen en de Kerstman gemaximaliseerd wordt. In de data heeft elk kind 10 voorkeuren voor zijn of haar cadeaus en de Kerstman heeft 1000 voorkeurskinderen voor elk cadeau dat beschikbaar is. Er zijn 1.000.000 kinderen en 1.000 verschillende cadeaus met elk 1.000 stuks. Geluk wordt gemeten door te kijken naar de positie van een cadeau in de voorkeurslijsten, hoe verder vooraan hoe hoger het geluk.

Wat het extra moeilijk maakt, is dat 0.4% van de kinderen een tweeling is en op verzoek van hun ouders hetzelfde cadeau moet krijgen.

Net een CQM-project

Ondanks dat het een fictief probleem is, lijkt het op ons dagelijks werk. De extra voorwaarden van bijvoorbeeld de tweelingen zorgen ervoor dat het geen tekstboekprobleem meer is. Wij hebben op de universiteit geleerd hoe we de tekstboekproblemen moeten oplossen en zijn vanuit de praktijk gewend om met ‘gekke’ extra voorwaarden om te gaan. Geen van onze klantprojecten is gelijk en dat vraagt creativiteit in oplossen. We gaan op zoek naar een mix van bekende oplossingstechnieken met op maat toegevoegde intelligentie. Wij zien in de verscheidenheid aan problemen de gemeenschappelijke deler en kunnen de verschillen in acht nemen.

Een aantal van onze projecten lijken op dit probleem. Zo hebben we voor een kinderopvangorganisatie een dag met workshops ingepland waarbij iedere deelnemer zijn eigen voorkeuren kon aangeven en er een zodanige toewijzing moest komen dat iedereen blij was met de toegewezen workshop maar de zaalcapaciteit niet werd overschreden. Andere voorbeelden van matchingproblemen uit onze praktijk betreffen het optimaal inzetten van financiële middelen bij het bouwen van een olieraffinaderij of het kiezen uit vervoersbedrijven die geboden hebben op een tender met transportritten.

Modelmatige kijk op dit probleem

Om dit probleem op te lossen doorlopen we de drie stappen van het optimalisatieproces: formulering van het probleem, vertaling naar wiskundig model, en het oplossen van het probleem. Hier vind je de blog over deze drie stappen.

De formulering van het probleem krijgen we in een competitie als deze cadeau. De regels, randvoorwaarden en doelstellingen staan vast. Dit is anders in de praktijkproblemen die we in ons dagelijks werk aanpakken. Daar is het helder krijgen van spelregels en doelstellingen een belangrijk deel van het werk.

Voor de vertaling naar wiskundig model, hebben we ervoor gekozen dit probleem te beschrijven als een min-cost-flow en dat doen we als volgt (zie ook het plaatje).

Begin met een bron waarin we 1 miljoen cadeaus tot ons beschikking hebben. Deze cadeaus laten we stromen naar de 1.000 verschillende cadeautypes. Hiervoor verbinden we de bron met elk cadeautype en staan op de verbinding een maximale hoeveelheid van 1.000 toe (hierdoor zijn er van elk type precies 1.000 exemplaren beschikbaar). Elk cadeautype verbinden we met elk kind. De maximale hoeveelheid over deze verbinding is 1. Tot slot verbinden we elk kind met de put waar de 1 miljoen cadeaus uitstromen. Op de verbinding tussen elk kind en de put is een maximale hoeveelheid van 1 (hierdoor krijgt ieder kind exact 1 cadeautje). Op de knopen van cadeautypes en kinderen is de instroom gelijk aan de uitstroom.

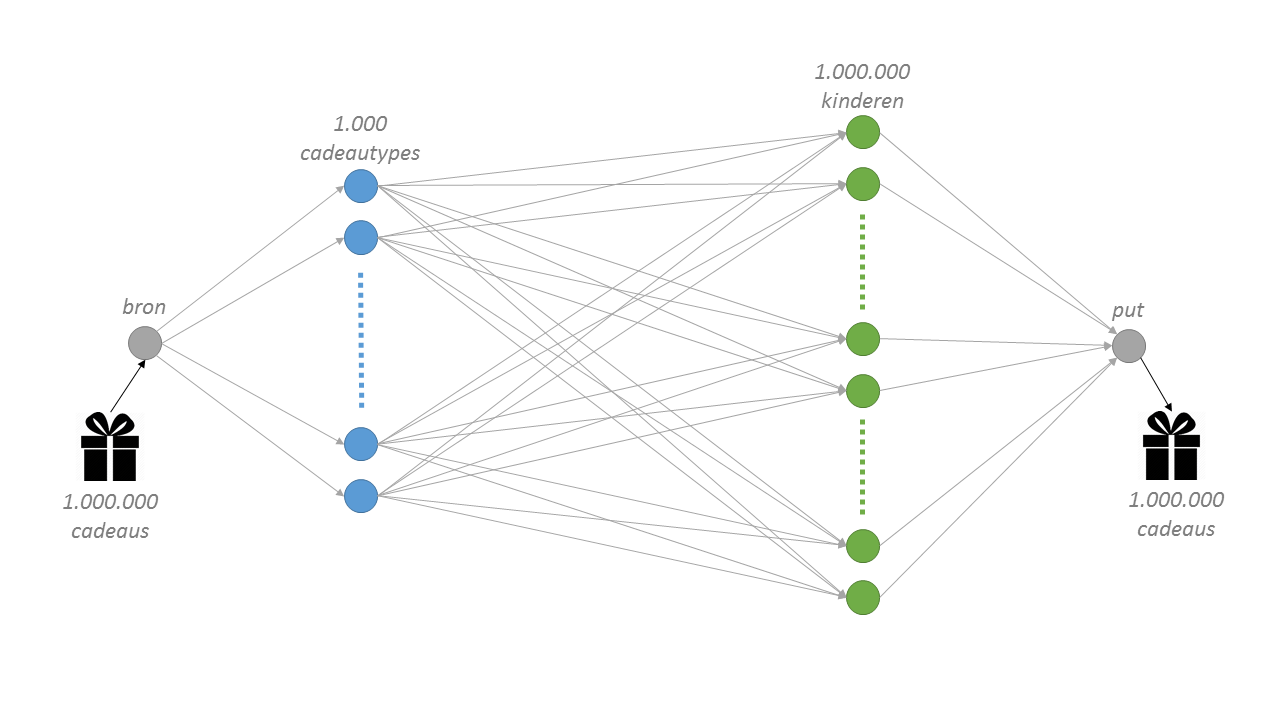
Als er 1 miljoen cadeautjes door dit netwerk gaan, kunnen we uit de verbinding tussen de cadeautypes en kinderen aflezen wie welk cadeau krijgt; een stroom van 1 tussen cadeau A en kindje X geeft aan dat kind X cadeau A krijgt. Door -1 x het geluk als kosten op de verbinding te zetten tussen cadeautypes en kinderen, geeft de stroom met minimale kosten de optimale oplossing. Zo’n min-cost-flow is een standaard probleem dat efficiënt op te lossen is.

Echter, nog twee problemen…

Er zijn echter twee problemen met het model dat hierboven beschreven staat:

1. Het netwerk is gigantisch. Met 1.000 cadeautypes en 1 miljoen kinderen bestaat het netwerk uit meer dan 1 miljard verbindingen. Dat is te veel voor een gewone computer om op te lossen. Het kost te veel geheugen en te veel tijd.
2. Er is ook nog niet afgedwongen dat een tweeling hetzelfde cadeau krijgt.

Het eerste probleem kunnen we aanpakken door het aantal verbindingen in het netwerk te reduceren. Er zijn twee manieren voor reductie:

• De voorkeurslijsten zijn relatief kort, en een ongewenst cadeautje kun je vervangen door een ander ongewenst cadeautje zonder dat de oplossing echt verandert. We laten dus alle verbindingen die niet op de voorkeurslijsten staan weg en vervangen dit door één generiek ongewenst cadeau.
• Twee kinderen die een tweeling vormen kunnen we samenvoegen tot 1 knoop. Dan moeten we de inkomende en uitgaande verbindingen wel capaciteit 2 geven. Er is gegarandeerd dat een tweeling dan twee cadeaus krijgt, maar nog niet dat het gelijke cadeaus zijn.

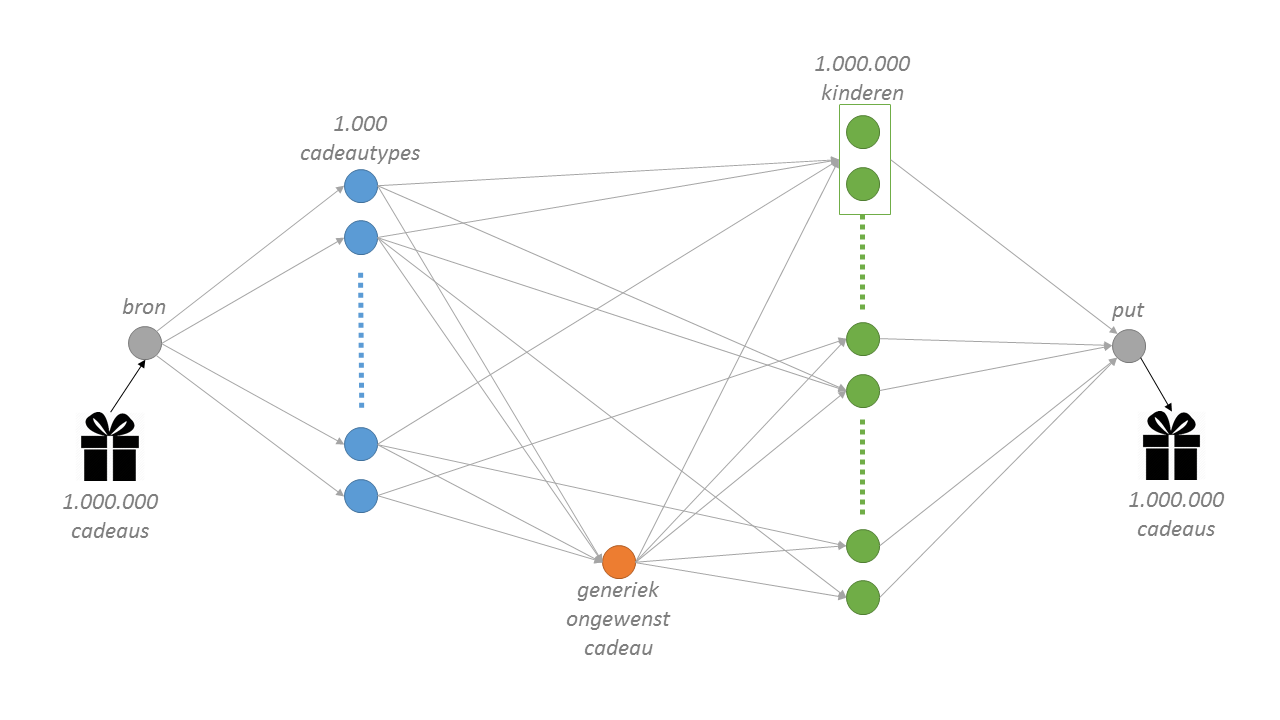
In dit nieuwe netwerk zijn er geen miljard verbindingen meer, maar slechts +/- 12 miljoen. Een enorme reductie waardoor het een oplosbaar probleem wordt.

Te gemakkelijk…

Dit probleem had CQM – net als een aantal andere deelnemers – binnen 1 week optimaal opgelost. Er was meer dan een maand de tijd om een goede oplossing in te zenden, maar we waren na een paar dagen al klaar. Door het probleem slim te modelleren zoals hierboven beschreven, en de resterende randvoorwaarde van de tweelingen te modelleren in een Mixed Integer Linear Program konden we aantoonbaar de beste oplossing vinden met behulp van de Gurobi software.

Dit gaf een dubbel gevoel; Het is het best haalbare resultaat met een hoge klassering, maar toch ook een beetje onbevredigend. Eigenlijk te gemakkelijk voor ons en niet zo moeilijk als we gewend zijn van Kaggle.

Nieuwe uitdaging

Als reactie op het snelle oplossen van de uitdaging heeft Kaggle besloten de competitie te herstarten maar dan net iets moeilijker. In de nieuwe uitdaging zijn de voorkeurslijsten langer gemaakt, er zijn nu 0.5% drielingen en 4% tweelingen en de maat voor geluk is complexer (niet-linear) gemaakt. En misschien wel het belangrijkste is een verbod op het gebruik van commerciële software.

Ook dit nieuwe probleem hebben we met de nieuwe spelregels opgelost, en de 7^de plek behaald.

Trots

Onze deelname heeft een 7^de plaats als resultaat en dat is een gouden Kaggle medaille waard. Een prestatie om trots op te zijn.

In eerdere edities wonnen we al een bronzen, een zilveren en een gouden medaille (zie afbeelding rechts). We laten daarmee weer zien dat we meedraaien in de wereldtop wat betreft het oplossen van complexe optimalisatieproblemen en data science vraagstukken.

We kijken al uit naar de volgende uitdaging: volgend jaar weer goud?!

 

Ook interessant om te lezen

• Een overzicht van voorgaande Kaggle Santa Challenges.
• Het 3-stappen optimalisatie process. 
• De uitdaging van Kaggle. 
• Open source solver voor min-cost-flow.