16/02/2017
In de projecten bij CQM gaat het niet altijd om cijfers maar soms juist om teksten. Bijvoorbeeld als het gaat om sentimentanalyse in reviews of om adresgegevens. Net als in de cijfermatige data zien we ook vaak fouten in tekstuele data. Ik heb adressenlijsten gezien waar meer dan 30% fout was! Dit is met een stukje slimme wiskunde razendsnel te herstellen. Lees hoe wij dit doen.
Welke stad bedoel je?
Iedereen die gebruik maakt van Google Maps kent de functionaliteit van Google die je helpt de juiste stad te vinden. Je opent Google Maps en typt EIDHOVN. Vrijwel direct verschijnt er een lijstje met suggesties, met bovenaan EINDHOVEN. Zoiets willen we allemaal wel, maar niet iedereen heeft de computerpower en informatieverzameling van Google tot zijn beschikking. Die zijn gelukkig niet nodig als je dit maar slim aanpakt.
Er zijn in Nederland zo’n 2500 steden en dorpen en het is voor een computer geen probleem om vast te stellen dat EIDHOVN er niet bij zit. Maar welke bedoel je dan wel? Om deze vraag snel te beantwoorden, heb je twee dingen nodig. Ten eerste een manier om de overeenkomst tussen twee woorden te meten, dit wordt een similarity measure genoemd. Ten tweede een manier om deze uit te rekenen op alle woorden. En dit laatste is het probleem. Het kost te veel tijd om met alle opties te vergelijken. Dat doen we slimmer met behulp van zogenaamde trigrams.
Selecteren met trigrams
Een trigram is een combinatie van drie letters. Dit is de sleutel om snel tot juiste kandidaten te komen bij een fout geschreven woord. Hoe dit werkt is het best uit te leggen aan de hand van een voorbeeld. We nemen het fout geschreven EIDHOVN en plakken er twee spaties voor en twee na. Neem vervolgens elke drie letter combinatie van het woord; dit zijn dan __E, _EI, EID, IDH, DHO, HOV, OVN, VN_ en N__. De spaties zorgen ervoor dat elke letter in precies 3 trigrams komt.
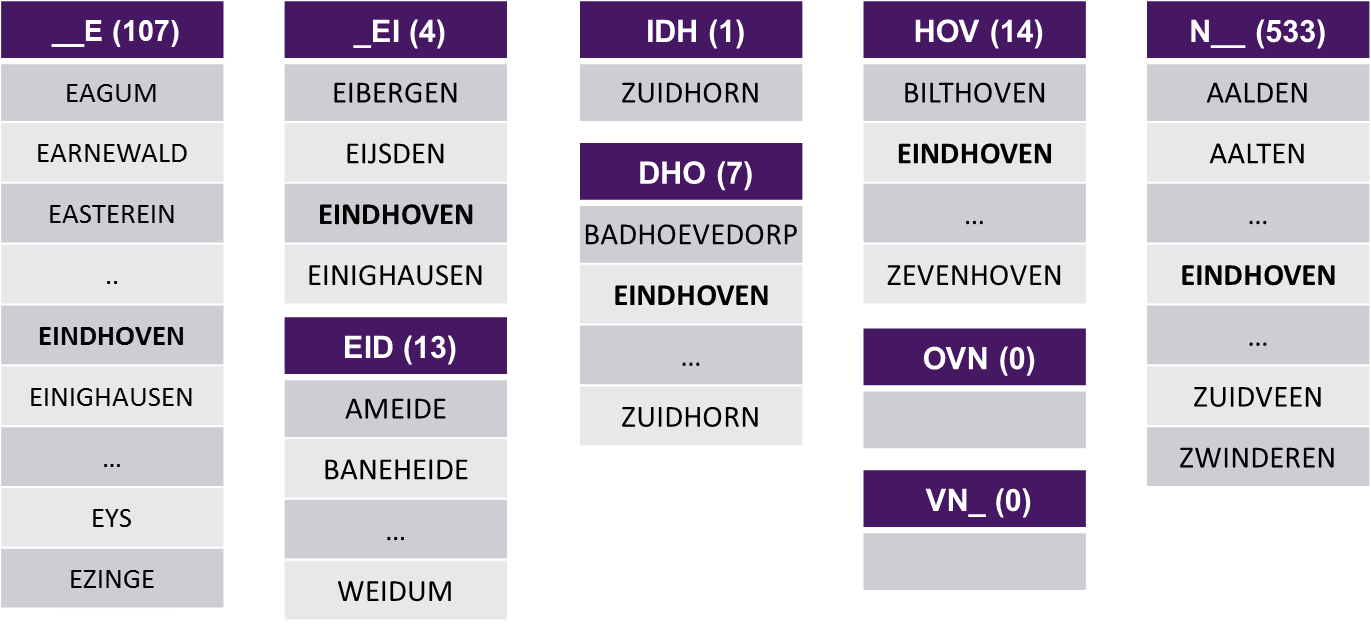
Met behulp van deze trigrams kun je een veel kleinere lijst van steden samenstellen die mogelijk bedoeld worden. Zo zijn er in Nederland maar 107 steden die met een E beginnen en dus __E als trigram bevatten, er zijn er maar 4 die met EI beginnen en dus _EI als trigram bevatten, etc. Sterker nog, er zijn maar 7 steden die minstens drie trigrams van het genoemde lijstje bevatten. Op deze manier hoeven we alleen de similarity measure op deze 7 steden uit te rekenen. De kritische lezer zal zich realiseren dat het nog niet zo eenvoudig is om snel deze selecties te maken.
Scoren met trigrams
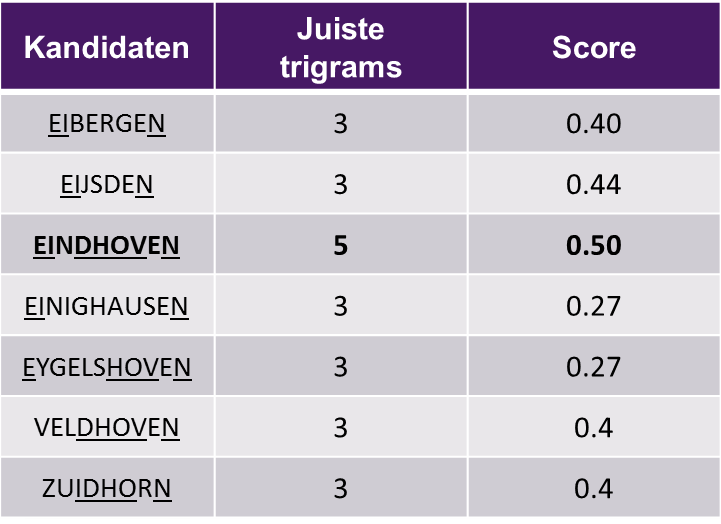
Met behulp van dezelfde trigrams is er een similarity measure ofwel een score te bepalen. Dit doen we door de score niet alleen te bepalen op het aantal overeenkomende trigrams, maar ook te koppelen aan de woordlengte, want dit blijkt het meest robuust te zijn tegen de verschillende soorten typefouten die we maken. We delen het aantal juiste trigrams door het gemiddelde aantal trigrams in EIDHOVN en de kandidaat. Het woord met de hoogste score is dan de winnaar. Natuurlijk komt EINDHOVEN hier als beste uit met een score van 0.50. (Vijf juiste trigrams en EINDHOVEN en EIDHOVN hebben 11 respectievelijk 9 dus gemiddeld 10 trigrams.)
Wat de kwaliteit van deze aanpak onderschrijft, is dat zelfs EIHOV gecorrigeerd wordt naar EINDHOVEN!
Toepassingen
Dit stukje slimme wiskunde kan typefouten herstellen en is niet alleen accuraat maar ook razendsnel. Op deze manier is het te gebruiken in planningssystemen waar de gebruiker binnen een aantal milliseconden geassisteerd wordt als er een typefout in een adres wordt gemaakt, zoals in de software van onze partner EVO-it is gedaan. Deze methode is echter veel breder toepasbaar en dan denk ik niet alleen aan spellingscontrole en tekstherstel, maar ook aan cryptografie en plagiaatdetectie.
- Wilt u meer weten over het herstellen van fouten in tekstuele data? Neem contact op met Jacob Jan, hij zal u graag helpen!
- Andere blogs van CQM lezen? U vindt ze hier.
- Of wilt u altijd op de hoogte blijven van het laatste nieuws van CQM? Volg ons dan op LinkedIn of schrijf u in voor de digitale nieuwsbrief (max. 4x per jaar).


