Prescriptive Analytics - Deel 2

26/06/2017

Deel 2: Integer linear programming voor de videoschouwtrein

Deze blogreeks gaat over prescriptive analytics. Deel 1 uit deze reeks beschrijft de 3 stappen van het optimalisatieproces. Deel 2 van deze reeks beschrijft een voorbeeld uit ons werkveld. Het voorbeeld gaat over de planning van de videoschouwtrein; het efficiënt filmen van de duizenden wissels van het Nederlandse spoorwegennet. Dit lossen we op met behulp van een wiskundige techniek die Integer Linear Programming heet.

Data Science is het moderne jasje waarin wij bij CQM (al ruim 35 jaar) met grote hoeveelheden data en met behulp van wiskundige modellen de structuren creëren om de juiste beslissingen te nemen. In data science termen heet het begrijpen van je data descriptive analytics, het voorspellen predictive analytics en het optimaliseren om de beste keuze te maken prescriptive analytics (zie ook deze blog).
 

Videoschouwtrein

De videoschouwtrein is een trein uitgerust met camera’s die de wissels op het spoorwegennet inspecteert, om zo opkomende defecten vroegtijdig te signaleren. Deze trein moet alle wissels af gaan en zo weinig mogelijk in de weg rijden van de andere treinen. NB. Dit is natuurlijk een sterk vereenvoudigde probleemstelling van het project  dat we werkelijk voor ProRail hebben uitgevoerd.


Hoe zien de 3 stappen van het optimalisatie proces er uit in het praktijkvoorbeeld van de videoschouwtrein?

1. Formulering van het bedrijfsprobleem

Een trein mag op het spoor alleen volgens vooraf vastgestelde routes over het spoor rijden. Deze routes zitten in het veiligheidssysteem van de verkeersleiding en afwijking hiervan zijn absoluut verboden. Routes lopen van het ene sein (= stoplicht) naar het andere. Het te maken plan bestaat dan ook uit een aantal routes die op elkaar aansluiten en het plan bezoekt elke wissel.

Het onderstaande spoorschema geef aan hoe de route van sein 72 naar sein 34 loopt op emplacement Apeldoorn.

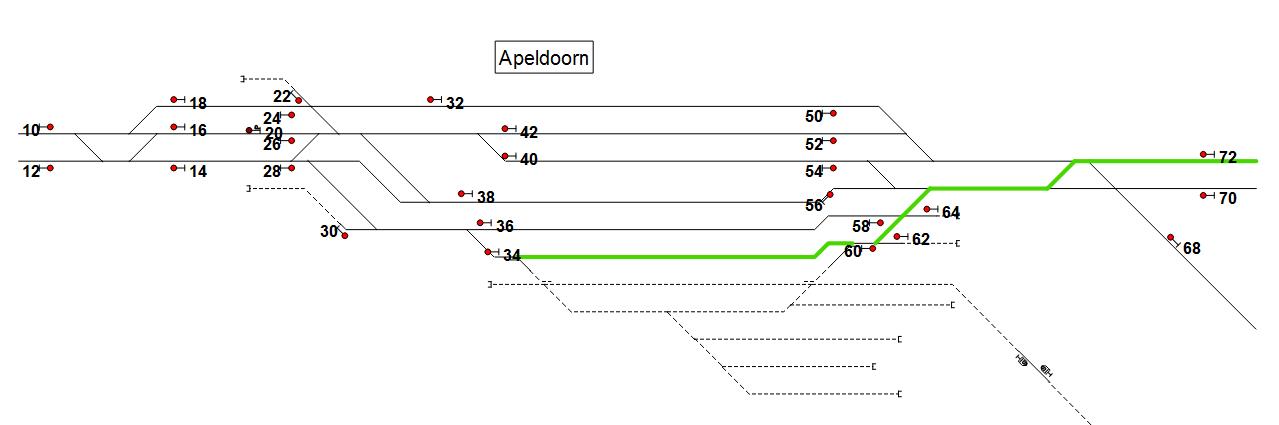
Het optimalisatieprobleem betreft hier het kiezen van routes onder twee randvoorwaarden. Ten eerste moeten de routes aansluiten en ten tweede moeten de geselecteerde routes alle wissels afdekken. De doelstelling is om dit in een zo kort mogelijke tijd te doen.

2. Vertaling naar een wiskundig model

Het bedrijfsprobleem formuleren we hieronder puntsgewijs én we voegen een wiskundig model toe.  

  • Beslis voor elke route hoe vaak deze geselecteerd wordt.
    Wiskundig: De variabele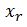geeft aan hoe vaak route r wordt geselecteerd.
  • Het aansluiten van de geselecteerde routes garanderen.
    Dit wordt in het wiskundige model in twee stappen geregeld. Ten eerste moeten er bij elk sein s even veel gekozen routes aankomen als vertrekken. In wiskundige notatie is dat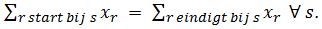  In de het tweede deel wordt met een subtour eliminatie geregeld dat het plan niet bestaat uit meerdere onderdelen die niet met elkaar verbonden zijn. De details hiervan laat ik even achterwege.
  • Het plan moet alle wissels afdekken.
    Van elke route r weten we of deze over wissel w gaat. De waarde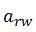 is 1 als r over w gaat en anders 0. De tweede randvoorwaarde luidt dan als volgt: voor elke wissel w geldt dat er ten minstens 1 route wordt gekozen die over deze wissel gaat. In wiskundige notatie is dat .
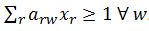  • De doelstelling is het minimaliseren van de totale rijtijd.
    Van elke route r kunnen we vooraf uitrekenen wat de rijtijd is, deze waarde noemen we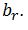  De totale tijd van het plan is de som van de rijtijd van de geselecteerde routes. Wiskundig beschreven is het doel dus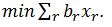 

3. Oplossen van het probleem

Het geformuleerde wiskundig model is van het type Integer Linear Program, omdat de variabelen geheeltallig (= integer) en de formules lineair zijn. Hiervoor bestaan zeer krachtige solvers zoals CPLEX en Gurobi. Met de modeleeromgeving van AIMMS is het wiskundige model eenvoudig aan een dergelijke solver aan te bieden en op te lossen.
 

Het resultaat

Met behulp van prescriptive analytics is de planning van de Videoschouwtrein met tientallen procenten verbeterd, zijn vele euro’s bespaard en hinder op andere treinen voorkomen! De wiskundige optimalisatie is ingebed in planningssoftware die naast deze berekeningen ook manuele interventies, visualisatie en printen van rittenboeken mogelijk maakt. We zijn er trots op dat de rittenboeken gemaakt met onze wiskundige modellen bij de machinist in de trein liggen.

Is optimalisatie een interessante toepassing van data science voor uw bedrijf? Neem dan contact op met Jacob Jan

 

Aanbevolen

 

Jacob Jan Paulus
Jacob Jan Paulus helpt je graag verder Neem contact op