Eindstand competitie: werking algoritme

30/04/2020

Blog 1 van 3

Enige tijd terug gaven we een spoiler alert en lieten we met ons algoritme zien hoe je de eindstand van de Eredivisie kunt voorspellen. Ook voor eigen competitie gedreven sporten kun je via onze tool de winnaar bepalen. We zijn met die blog opgepikt door Omroep Brabant, Voetbal Primeur en overige media. We hebben veel leuke reacties ontvangen en ook een aantal kritische. Want, het Dick Advocaat-effect is natuurlijk niet meegenomen, net zoals blessures. Onze werkwijze om tot de voorspellingen te komen bestaat uit drie stappen, namelijk: 1. het schatten van de kwaliteit en het thuisvoordeel van ieder team, 2. het simuleren van het resterende competitieprogramma en tot slot 3. het vertalen van de resultaten naar ranking en kansen. In een drieluik blog geven we de methodologische achtergrond van onze tool en vertellen we je waarom we bepaalde keuzes hebben gemaakt. In deze blog lichten we stap 1 toe: het schatten van de kwaliteit en thuisvoordeel van ieder team.


Schatten kwaliteit en thuisvoordeel

Laten we beginnen met de input voor het model. Die bestaat uit een Excel met 4 kolommen waarin alle reeds gespeelde wedstrijden zijn weergegeven. In Figuur 1 staat een snapshot van de input, welke je vervolgens upload in onze tool.


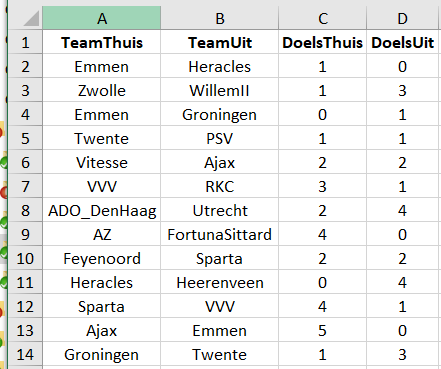
Figuur 1 Snapshot modelinput.

Op basis van de reeds gespeelde wedstrijden wordt bepaald welke wedstrijden er nog gespeeld moeten worden. Meestal spelen alle teams één keer uit en één keer thuis tegen elkaar, voor Basketbal spelen alle teams 2x thuis en 2x uit. Deze input wordt gebruikt om het volgende model – het model van Koning – te schatten(*1):

Y­ij = Ki – Kj + Ti + εij

Hierbij is Yij het doelpuntenverschil in een individuele wedstrijd waarin team i thuis speelt tegen team j. Als de uitslag 3-1 is in het voordeel van team i, dan geldt dus dat Yij = 2. Als uitspelend team j de wedstrijd wint met 4-2 dan zou gelden dat Yij = -2. Teams i en j zitten in de verzameling C van competitieteams. We noemen het aantal teams in de competitie N. 

Verder staat Ki voor de kwaliteit van team i, Kj voor de kwaliteit van team j, en Ti voor het thuisvoordeel van team i. εij is normaal verdeeld met verwachting 0 en vaste variantie σ2 en beschrijft het toeval en alle andere mogelijke effecten die de werkelijke uitslag van een wedstrijd beïnvloeden.

Het verschil (Ki – K j) kan dus geïnterpreteerd worden als het verwachte doelpuntenverschil in de uitslag als teams i en j op neutraal terrein tegen elkaar spelen.


Kleinste-kwadratenmethode en parameters

We schatten de parameters in dit model met de kleinste-kwadratenmethode. De parameters die geschat worden zijn dus voor ieder team in de competitie Ki en Ti en daarnaast σ voor de competitie als geheel. Dit zijn in totaal (2N+1) parameters. De output van het regressiemodel bestaat dus uit schattingen voor parameters (Ki,Ti)i=1,..N en σ, zeg (ki,ti) en s respectievelijk.

Het is eenvoudig in te zien dat er nog een normalisatie nodig is om tot één unieke oplossing te komen. We leggen, net als Koning, de voorwaarde op dat het gemiddelde van alle geschatte kwaliteitsparameters ki gelijk is aan 0. Een hypothetisch gemiddeld team heeft dus kwaliteit Ki = 0.

Dit maakt dat ki geïnterpreteerd kan worden als het verwachte doelpuntenverschil in een wedstrijd van team i op neutraal terrein tegen een gemiddeld team. Als ki positief is dan is team i beter dan het gemiddelde team en bij ki negatief is team i minder goed dan het gemiddelde team.

Dit is een standaard regressiemodel met de bijbehorende eisen om alle parameters te kunnen schatten. Omdat we dit model in deze toepassing gebruiken voor competities die over de helft zijn, is in de praktijk altijd (ruimschoots) aan die noodzakelijke voorwaarden voldaan. Dit laatste mede ook doordat in de opzet van speelschema’s getracht wordt om gedurende het jaar teams in enigszins gelijke mate uit en thuis te laten spelen.


De uitslag van de Eredivisie

In tabel 1 staan ook de geschatte model parameters voor de eredivisie van 2019-2020 op basis van de reeds gespeelde wedstrijden voor de Corona uitbraak. De schatting voor σ is 1.74. We gebruiken hiervoor de Root Mean Squared Error uit de regressieresultaten.


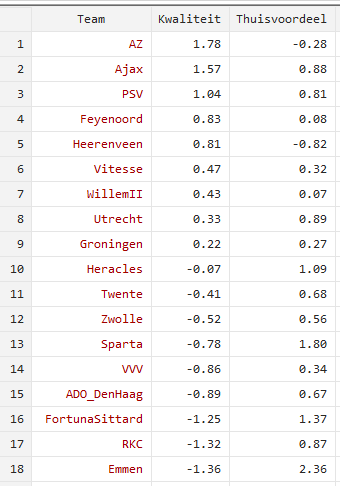
Tabel 1 Geschatte parameters Eredivisie 2019-2020.

We zien in Tabel 1 dat wanneer alle wedstrijden op neutraal terrein zouden worden afgewerkt, AZ het sterkste zou zijn en Emmen nog net onder RKC zou eindigen. We zien echter dat Ajax en vooral ook Emmen een zeer sterk thuisvoordeel hebben. Dit thuisvoordeel speelt in de helft van de wedstrijden een rol, namelijk alle thuiswedstrijden. Daarmee compenseren Emmen en Ajax hun iets lagere kwaliteitsscore.


Voorbeeld: Vitesse – Twente en de uitslag

Laten we een ander voorbeeld nemen. Als Vitesse thuis speelt tegen Twente dan is het verwachte doelpuntenverschil in de uitslag:

Vitesse – Twente: 0.47 – (-0.41) + 0.32 = 1.20

Dat betekent dat wanneer Vitesse heel vaak thuis zou spelen tegen Twente, Vitesse gemiddeld met 1.2 doelpunten verschil zal winnen. De spreiding hierop is 1.74.

Dit betekent dat we verwachten dat bijvoorbeeld 95% van de wedstrijden een uitslag zal hebben waarvan het doelpuntenverschil in het interval [-2.2 ; 4.6] zit. Je zou dit kunnen interpreteren als dat een echt bijzondere uitslag een uitslag zou zijn waarin Twente met drie of meer doelpunten verschil wint of Vitesse met 5 of meer doelpunten verschil wint (*2).

In Tabel 2 beschrijven we volgens dezelfde logica de kans dat een wedstrijd eindigt in een gelijkspel, winst voor Vitesse en winst voor Twente (*3).


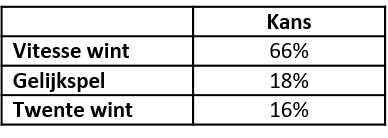
Tabel 2 Kans op verschillende winnen en gelijk spelen.


Voorbeeld 2: het ingestorte dak van AZ

In de toelichting op Tabel 1 beschreven we al de essentiële rol van thuisvoordeel in de bepaling van de eindstand en het voordeel dat Ajax en vooral ook Emmen daardoor hebben op hun concurrenten. Een interessante vraag die zich aandient is de volgende: wat zou er gebeurd zijn als AZ haar thuiswedstrijden in eigen stadion zou hebben afgewerkt? Oftewel: heeft het ingestorte dak AZ de titel gekost?

Als AZ een substantieel thuisvoordeel zou hebben behaald door in Alkmaar te spelen, dan zou AZ kampioen zijn geworden en niet Ajax, dus het antwoord op die vraag zou zomaar “ja” kunnen zijn. Echter, het is opvallend dat Heerenveen een groot thuisnadeel (*4) heeft zonder dat daar een duidelijke verklaring voor is dus een zekerheid is het niet.


Het roept veel vragen op

Bovenstaande beschrijft de modellogica waarmee we op basis van de reeds gespeelde wedstrijden kwaliteit, thuisvoordeel en onzekerheid bepalen. Met behulp van Monte Carlo simulatie bepalen we alle resultaten. In een vervolgblog beschrijven we op welke manier we dat doenen gaan we dus dieper in op deel 2 van de methodologie: het simuleren van het resterende competitieprogramma. En tot slot, in het derde en laatste deel van deze reeks, laten we zien hoe we op basis van die kansverdelingen de verwachte eindstand bepalen.

Heb je vragen of wil je meer informatie? Neem dan contact op met Jan Willem Bikker.


We hebben nog veel vragen die we interessant zouden vinden om beantwoord te krijgen, zoals onder andere ‘hoeveel beter wordt het model als er competitiegedreven aspecten worden toegevoegd’ en ‘hoe groot zou het thuisvoordeel van AZ moeten zijn om te winnen’? Ken je publicaties die hierover gaan of zie je graag zelf een vraag beantwoord, neem dan vooral ook contact met ons op :)

 
Verwijzingen in deze blog:
[*1] Dit model wordt beschreven in “Oost, west, thuis best”, Ruud H. Koning, Stator, Jaargang 9 nr 2; Juli 2008; blz 12-15. Zie https://www.vvsor.nl/wp-content/uploads/2018/01/STAtOR_2008-2_totaal.pdf.
[*2] Wij zijn ons ervan bewust dat een uitslag als 8-7 in het voordeel van Vitesse ook heel bijzonder is in de praktijk. Maar dan niet zozeer vanwege het doelpuntenverschil maar vanwege het totaal aantal gescoorde doelpunten in de wedstrijd. Deze vorm van bijzondere uitslag laten we hier buiten beschouwing. In https://www.vvsor.nl/wp-content/uploads/2018/01/STAtOR_2013-2_totaal.pdf gaan Loek Groot en Marnix Zoutenbier daar wel op in (blz 4-8).
[*3] Als een specifieke uitslag in het interval [-0.5;0.5) ligt dan is dat een gelijkspel. Als de uitslag ≥0.5 is dan wint het thuisteam en als de uitslag <-0.5 is dan wint het uitteam. Bij sporten, zoals basketbal, waar een gelijkspel geen mogelijke uitkomst is geldt vergelijkbaar dat als de uitslag <0 is dat het uit team wint en bij een uitslag ≥0 wint het thuis team. In praktische simulaties komt een uitslag die exact 0 is niet voor.
[*4] De interpretatie van thuisvoordeel is subtiel. Een negatief thuisvoordeel wil niet zeggen dat een team het thuis in de wedstrijduitslagen slechter heeft gedaan dan uit. In uitwedstrijden doet een team het namelijk (ook) slechter vanwege het thuisvoordeel van de tegenstander in die wedstrijd. Dus als alle teams op één na een thuisvoordeel hebben, dan zal dat ene team zonder thuisvoordeel het in thuiswedstrijden tóch beter doen dan uit.
Jan Willem Bikker
Jan Willem Bikker helpt je graag verder Neem contact op